|
Поскольку массы кубика и пластинки, сделанных из одного материала, одинаковы, то одинаковы и их объемы. Значит, при полном погружении в воду на них действует одна и та же выталкивающая сила. |
|
Плотность мрамора меньше плотности меди, поэтому при одинаковой массе мрамор имеет больший объем, значит, на него будет действовать большая выталкивающая сила и его легче удержать в воде, чем медную гирю. |
|
В романе Жюля Верна «80 000 километров под водой» есть такое место: «"Наутилус" стоял неподвижно. Наполнив резервуары, он держался на глубине тысячи метров... Я отложил книгу и, прижавшись к окну, стал всматриваться. В жидком пространстве, ярко освещенном электрическим прожектором, виднелась какая-то огромная неподвижная черная масса... "Это корабль!" -вскричал я». Нет, если корабль скроется под водой, он обязательно опустится на дно. |
|
Столько же, если пренебречь изменением плотности воды на различных глубинах. Тело опускается на дно сосуда, когда действующая на него сила тяжести больше выталкивающей силы. |
|
Закон Паскаля действует. Архимедова сила в условиях невесомости отсутствует. |
|
Больше или меньше получается при этом значение плотности? Прилипшие пузырьки воздуха незначительно увеличивают массу тела, но существенно увеличивают его объем. Поэтому значение плотности получается меньшим. |
|
Такое же, как и на Земле: архимедова сила равна весу жидкости, вытесненной погруженным в нее телом. |
|
Гири должны быть из того же вещества, что и взвешиваемое тело. |
|
При вдохе пловец всплывает, при выдохе погружается глубже в воду, так как при дыхании меняется
объем грудной клетки и соответственно меняется архимедова сила. |
|
Одинаковы. Брусок плавает в обеих жидкостях, значит, выталкивающая сила в каждой из них равна действующей на него силе тяжести. |
|
Нет, так как подъемная сила (разность между максимальной архимедовой силой и силой тяжести) круга имеет ограниченную величину |
|
Чтобы увеличить силу тяжести и сделать ее больше архимедовой силы, иначе водолаз не погрузится на необходимую глубину. |
|
Давление увеличится, так как повысится уровень воды в сосуде. |
|
Не изменится, так как вес куска дерева равен весу вытесненной им (и вылившейся из стакана) воды. |
|
|
|
Справедлив, так как вес поплавка равен весу вытесненной им жидкости. |
|
При одинаковых шариках уровень соприкосновения воды со ртутью не изменится. |
|
Вес плавающего стакана увеличится на вес изъятой из сосуда воды. Поэтому стакан будет погружен в воду немного глубже, так что уровень воды в сосуде не изменится. |
|
Вес плавающего льда равен весу вытесненной им воды. Поэтому объем воды, образовавшейся при таянии льда, будет в точности равен объему вытесненной им воды, и уровень жидкости в стакане не изменится. Если в стакане находится жидкость более плотная, чем вода, то объем воды, образовавшейся после таяния льда, будет больше, чем объем жидкости, вытесненной льдом, и вода перельется через край. Наоборот, в случае менее плотной жидкости, после того как лед растает, уровень понизится. |
|
|
|
Может. Например, лед в воде плавает, а в керосине тонет. |
|
Так как плотность пресной воды меньше плотности соленой, то повысился бы. |
|
|
|
Будет плавать. |

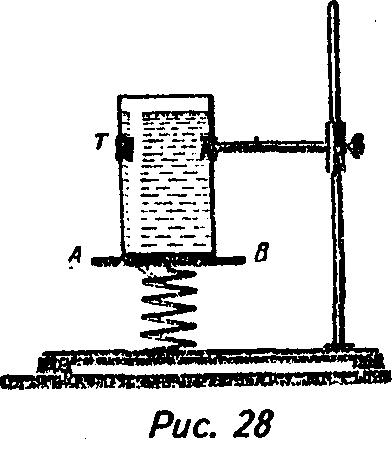 Задачу можно решить двумя способами. Первый: на дно цилиндрического сосуда действует, кроме веса воды, еще и вес плавающего в ней куска дерева, поэтому пластинка отпадет.
Второй, погруженный в воду кусок дерева повышает уровень воды в сосуде, от этого увеличивается гидростатическое давление на дно сосуда, значит, увеличивается действующая на пластинку сила, поэтому пластинка отпадет.
Задачу можно решить двумя способами. Первый: на дно цилиндрического сосуда действует, кроме веса воды, еще и вес плавающего в ней куска дерева, поэтому пластинка отпадет.
Второй, погруженный в воду кусок дерева повышает уровень воды в сосуде, от этого увеличивается гидростатическое давление на дно сосуда, значит, увеличивается действующая на пластинку сила, поэтому пластинка отпадет.
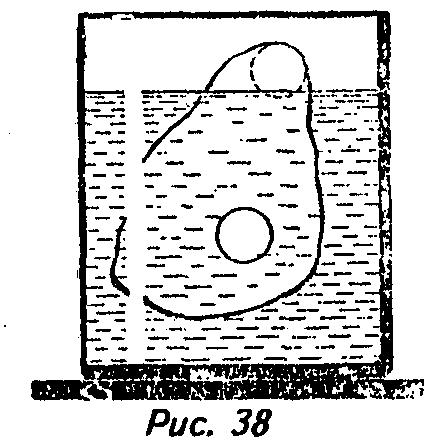 Объем количества воды, уравновешивающего свинец, в 11,3 раза больше объема грузика, ибо в 11,3
раза плотность свинца больше плотности воды. Если теперь лед растает, то погрузившийся в воду кусочек свинца, конечно, не заполнит собой той добавочной полости, которую занимал нагруженный лед. И уровень воды опустится.Пусть теперь кусок плавающего в воде льда, содержащего внутри себя пузырек воздуха, вытесняет определенный объем воды (рис. 38). Очевидно, вес льдинки не изменится, если пузырек переместится вверх, а свободная полость заполнится льдом. Но если вес льдинки не изменился, то сохранится прежним и объем вытесненной ею воды. Теперь
решение задачи сведено к случаю, описанному в предыдущем задаче, решение которой от формы куска льда не зависит. Поэтому уровень воды после таяния льда не изменится.
Объем количества воды, уравновешивающего свинец, в 11,3 раза больше объема грузика, ибо в 11,3
раза плотность свинца больше плотности воды. Если теперь лед растает, то погрузившийся в воду кусочек свинца, конечно, не заполнит собой той добавочной полости, которую занимал нагруженный лед. И уровень воды опустится.Пусть теперь кусок плавающего в воде льда, содержащего внутри себя пузырек воздуха, вытесняет определенный объем воды (рис. 38). Очевидно, вес льдинки не изменится, если пузырек переместится вверх, а свободная полость заполнится льдом. Но если вес льдинки не изменился, то сохранится прежним и объем вытесненной ею воды. Теперь
решение задачи сведено к случаю, описанному в предыдущем задаче, решение которой от формы куска льда не зависит. Поэтому уровень воды после таяния льда не изменится.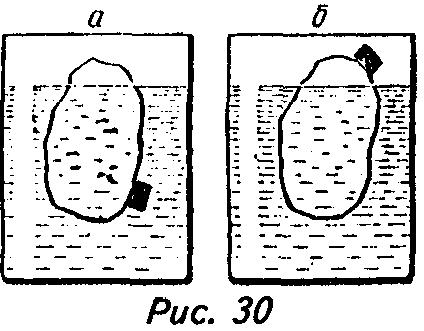 В обоих случаях уровень воды после таяния льда не изменится. В самом деле, суммарный вес воды, льда и пробки будет равен суммарному весу воды и пробки после того, как лед растает. Давление на дно сосуда не изменится, а значит, не изменится и высота уровня воды в сосуде.
В обоих случаях уровень воды после таяния льда не изменится. В самом деле, суммарный вес воды, льда и пробки будет равен суммарному весу воды и пробки после того, как лед растает. Давление на дно сосуда не изменится, а значит, не изменится и высота уровня воды в сосуде.